强化学习中值迭代算法的实现
重点
算法实现的重点是理解:值迭代算法和策略迭代算法都是交替进行value update和policy update,来求解最优策略。
两个策略的原理具体可以参考文章
什么是值迭代和策略迭代算法?
一、算法通俗讲解
目标:通过不断更新状态的价值函数,最终找到最优策略(即在每个状态下选择收益最大的动作)。
核心概念
迭代链路:$ V_{0} \to \pi_{0} \to V_{1}\to \pi_{1}\dots $
其中V代表每轮迭代中状态的state value,π代表策略。
已知条件
- 初始化的状态值函数 V(s):表示从状态
s出发,长期能获得的累计奖励期望。 - 状态转移概率 P(s’|s,a):在状态
s执行动作a后,转移到状态s'的概率。 - 奖励分布 p(r|s,a):在状态
s执行动作a后,获得即时奖励r的概率。
未知条件(要求解的值)
- 动作值函数 q(s,a):表示在状态
s下执行动作a后,能获得的累计奖励期望。
值迭代算法伪代码
初始化
对所有状态s,设定初始值V(s) = 0(或随机值)。循环更新直至收敛

关键注意事项
里面的变量V代表state value,在每轮迭代中的值都不一样,实际编程需要加上迭代轮次k。
停止迭代的条件,是评估两轮之间的V的差值是否足够小,$\theta$ 是一个很小的数,实际计算是通过求差值的最大值小于$\theta$来实现控制条件$ \left | V_{k+1} - V_{k} \right | \le \theta $求的是。
与策略迭代的区别
- 值迭代:直接更新值函数,策略是隐式的(通过取最大值得到),通常更快收敛。
- 策略迭代:显式维护策略,交替进行策略评估和策略改进,计算量更大。
二、python实现
def value_iteration(grid, theta=1e-4, max_iter = 1000):
#值迭代算法
#初始化state 函数
V = np.zeros((grid.rows, grid.cols))
for Iter in range(max_iter):
delta = 0
new_V = np.copy(V)
print("---------Iter------------", Iter)
for i in range(grid.rows):
for j in range(grid.cols):
state = (i,j)
if state in grid.terminal_states:
#终止状态不更新
#动作为原地不动
new_V[i,j] = 1.0 + grid.gamma*V[i,j]
continue
#计算所有可能动作的值函数
max_value = -np.inf
for action in grid.actions:
next_state = grid.get_next_state(state, action)
reward = grid.get_reward(state, next_state, action)
#贝尔曼最优方程更新 求解statue value
value = reward + grid.gamma * V[next_state]
if value > max_value:
max_value = value
new_V[i,j] = max_value
delta = max(delta, abs(new_V[i,j]-V[i,j]))
#打印当前state value和策略
V = np.copy(new_V)
print("当前的state value:\n",V)
iter_policy = extract_policy(grid, V)
print("当前策略:\n", iter_policy)
print("debug delta", delta)
if delta < theta:
break
return V
关键注意事项
- 收敛条件:通过计算两次迭代间
V(s)的最大差值(delta)判断是否终止。 - 效率优化:实际编程时需存储新旧两套
V值,避免在更新过程中覆盖旧值。 - 折扣因子 γ:通常取 0.9~0.99,控制未来奖励的重要性。
value_iteration函数是我们的值迭代算法的核心代码。现在我们以网格世界为例子,了解这个算法是怎么找到最优策略的。
三、一个简单的网格世界例子
网格世界中,agent需要找到到达终点的最优策略。
首先我们有第一种最简单的网格,就是只有一个终点,并且奖励函数也比较简单,到达终点奖励1,其他状态奖励0。

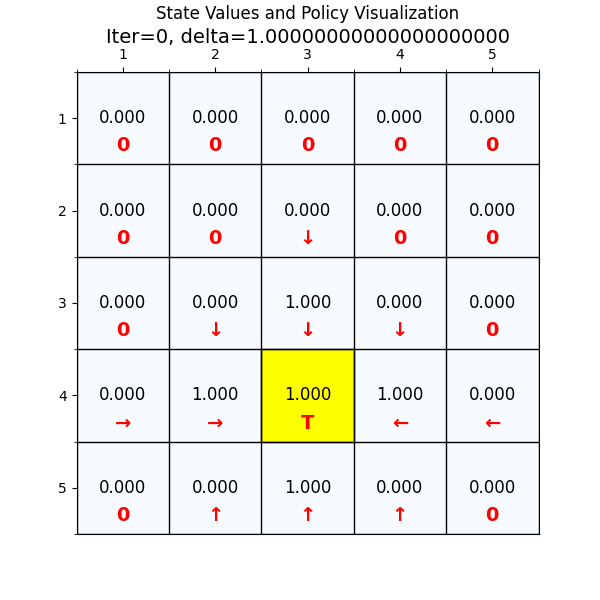
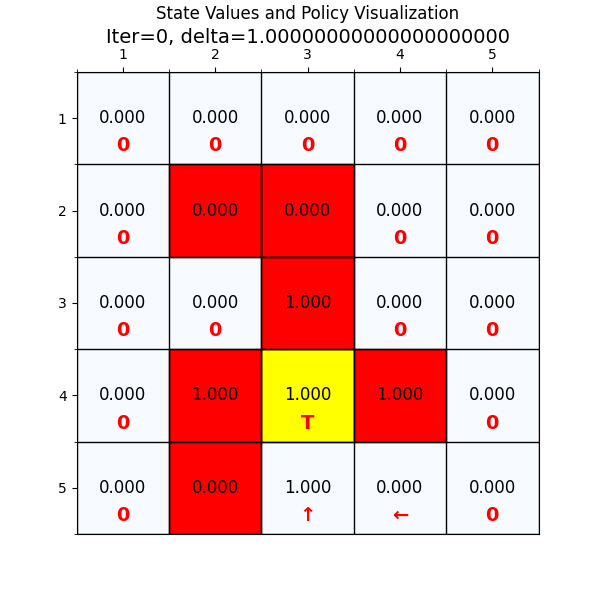
从图2中可以看到,经过一次迭代之后,部分网格中的state value已经从初始值0改变为1.0。
网格中的箭头,代表agent在这个state找到的最优方向,没有箭头的代表算法现在还没有计算到。
我们可以看到刚开始的时候,大部分state value都是0。state value=1.0的网格有五个,坐标分别是(3,3),(4,2),(4,4),(5,3)和终点(4,3)。
使用贝尔曼方程验证算法结果
那么为什么1轮迭代之后,这些网格的state value是1.0呢?
下面我们通过代码和贝尔曼方程计算一下。
首先从上节课回顾state value的定义:
状态价值函数:state value function也叫做**state value 对应标识V ,这个V和状态函数s和策略π有关,代表在给定策略π的情况下,状态s的期望价值(从当前状态开始到最终状态时走完一条trace,agent所获得的累加回报的期望。)
return的定义:return是从某个时刻开始,agent未来获得的所有奖励的累计值。在数学上用Gt表示。
公式如下:
$$
G_{t}= R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} + \dots
$$
先看下终点网格(4,3),由于是终点,所以及时奖励$R_{t+1}=1$,当agent到达终点时,我们肯定是期望agent保持在这个位置,所以$R_{t+2},R_{t+3}$都是对应状态(4,3)的value,由于初始化V=0,第一轮迭代时,$V_{0}[4,3]=0$
所以
$$
\begin{align}
V_{1}[4,3] &=1+\gamma V_{0}[4,3] + \gamma^2 V_{0}[4,3] + \dots \
&=1+0+0 + \dots \
&=1
\end{align}
$$
在看下网格(3,3),由于策略是向下,所以及时奖励$R_{t+1}=1$,由于初始化V=0,第一轮迭代时,$V_{0}=0$ 所以$R_{t+2},R_{t+3}$无论是哪个状态s的value 值都是0。
$$
\begin{align}
V_{1}[3,3] &=1+\gamma R_{t+2}+\gamma^2 R_{t+3} + \dots \
&=1+0+0 + \dots \
&=1
\end{align}
$$
对应网格(3,3)我们可以看到如果agent选择其他动作(’0’,’↑’, ‘←’, ‘→’)对应的及时奖励都是0,所以按照value 迭代的算法,策略会被更新为奖励最大的动作,即’↓’,也是图2中展示的策略。
同样对应其他网格(4,2),(4,4),(5,3)可以同样计算。
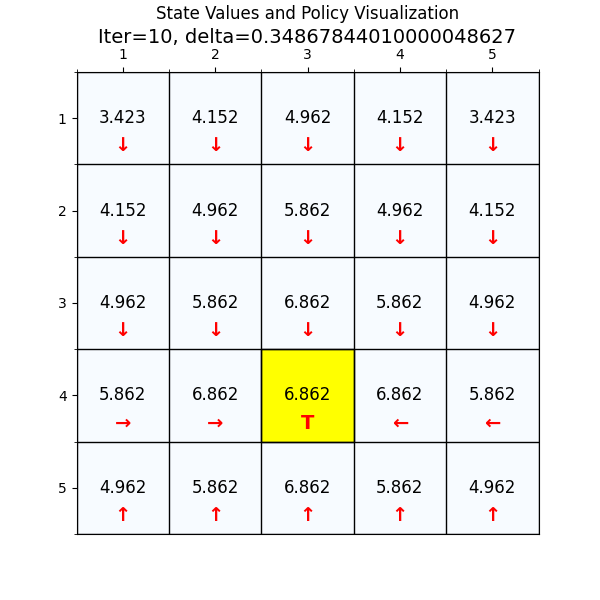
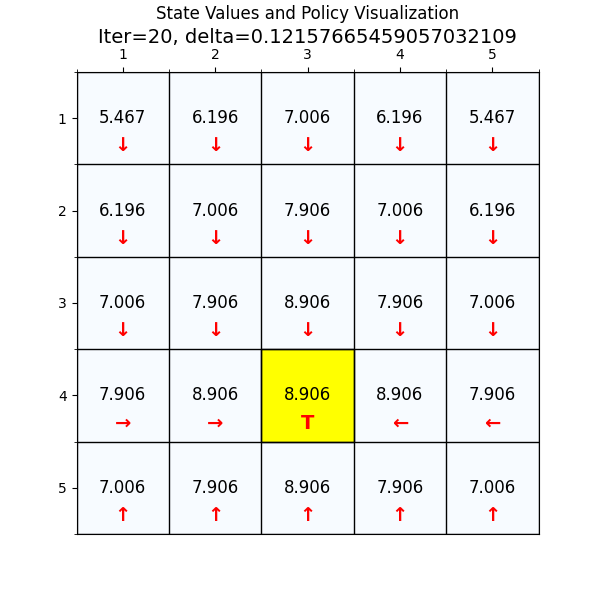
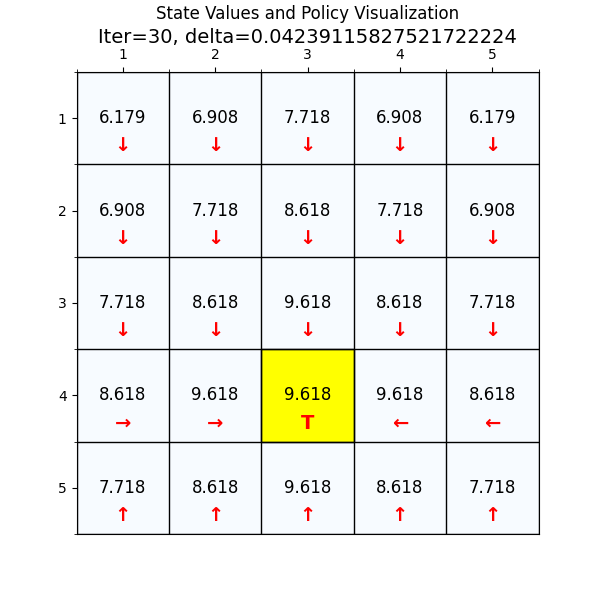
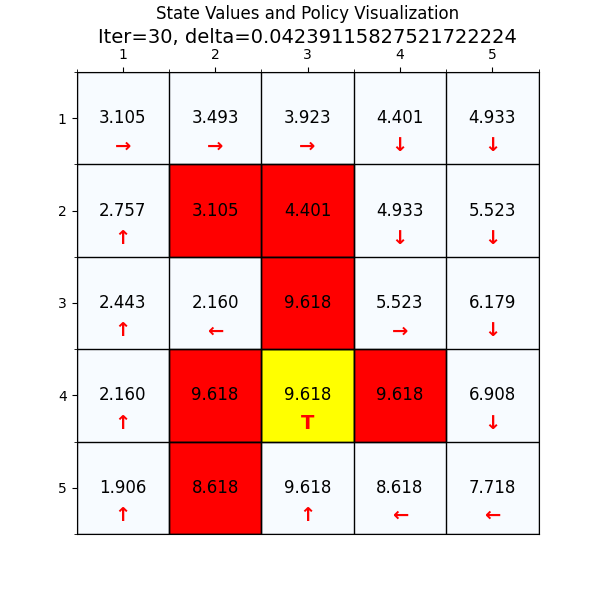
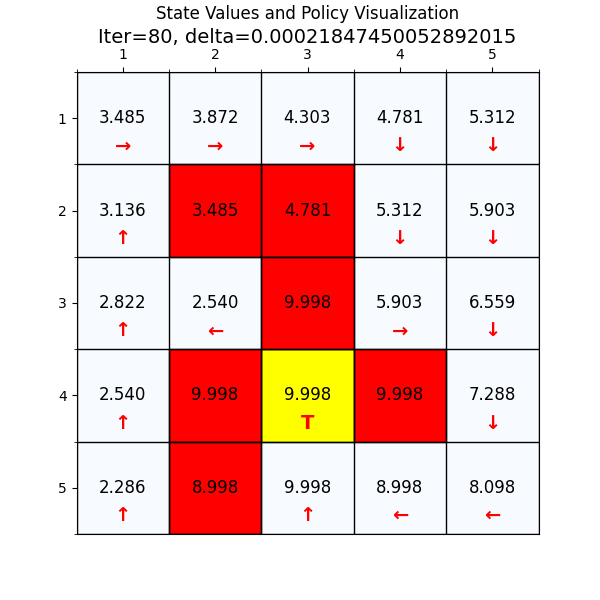
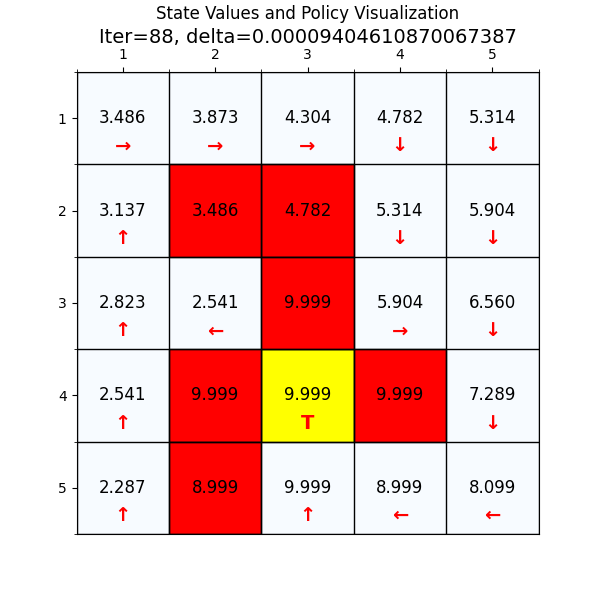
最优策略
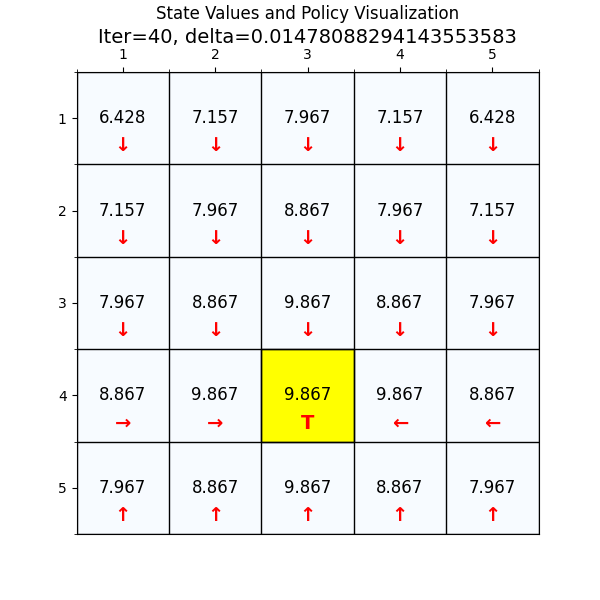
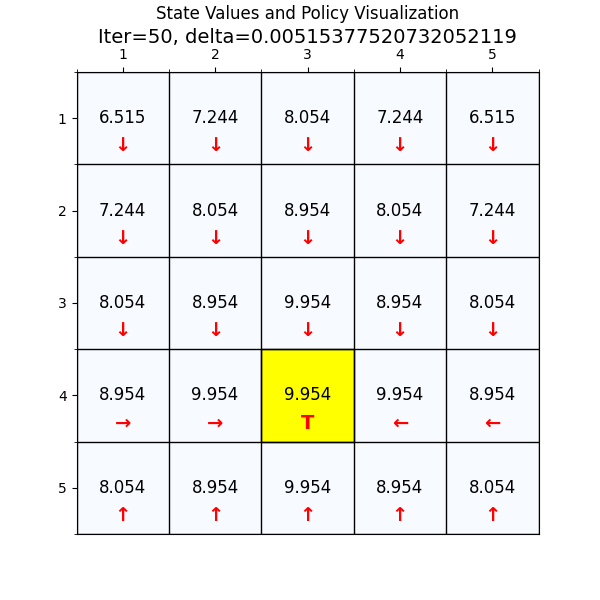
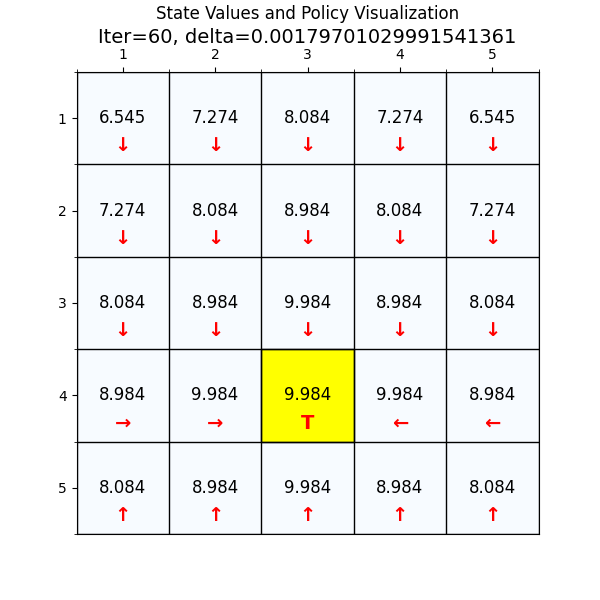
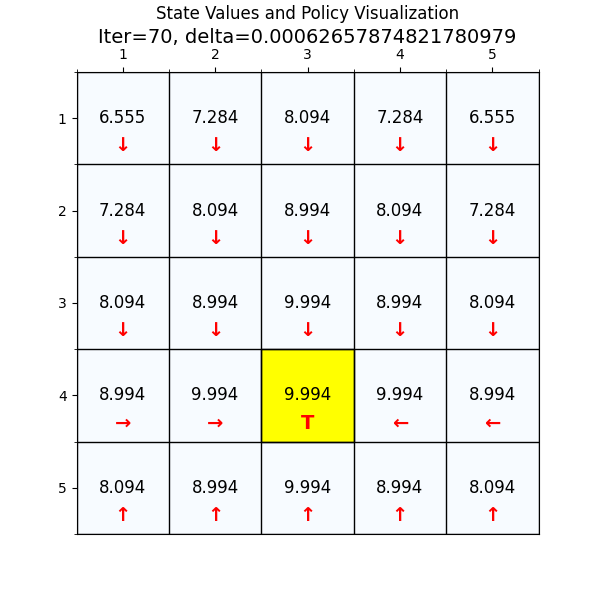
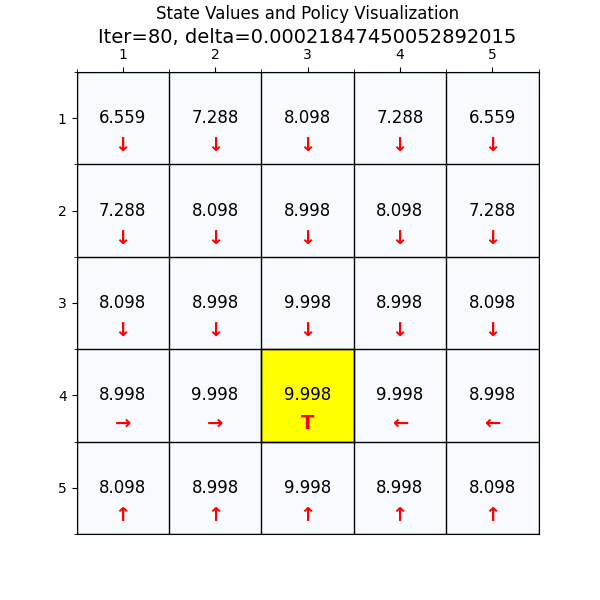
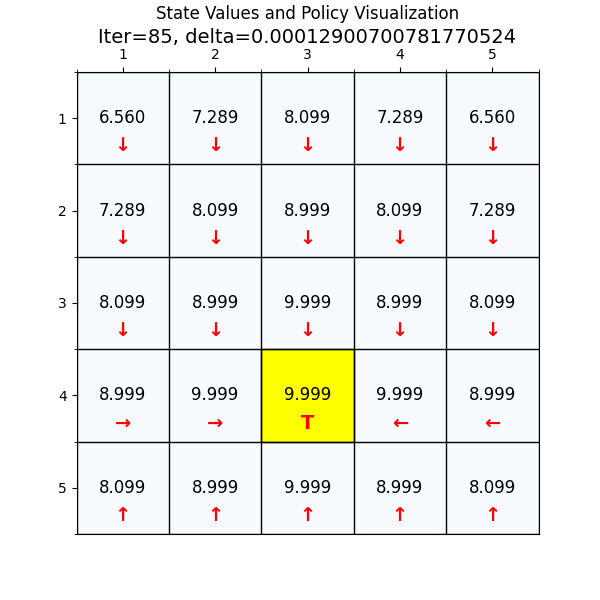
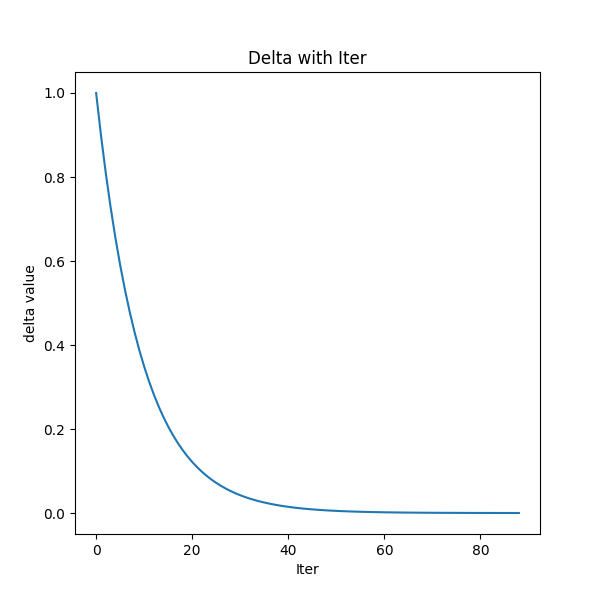
最终经过88次迭代之后,delta已经到了我们规定的最小值,state value也基本上没有变化了,说明我们已经找到了最优值。下面看一下最优策略和对应的state value。
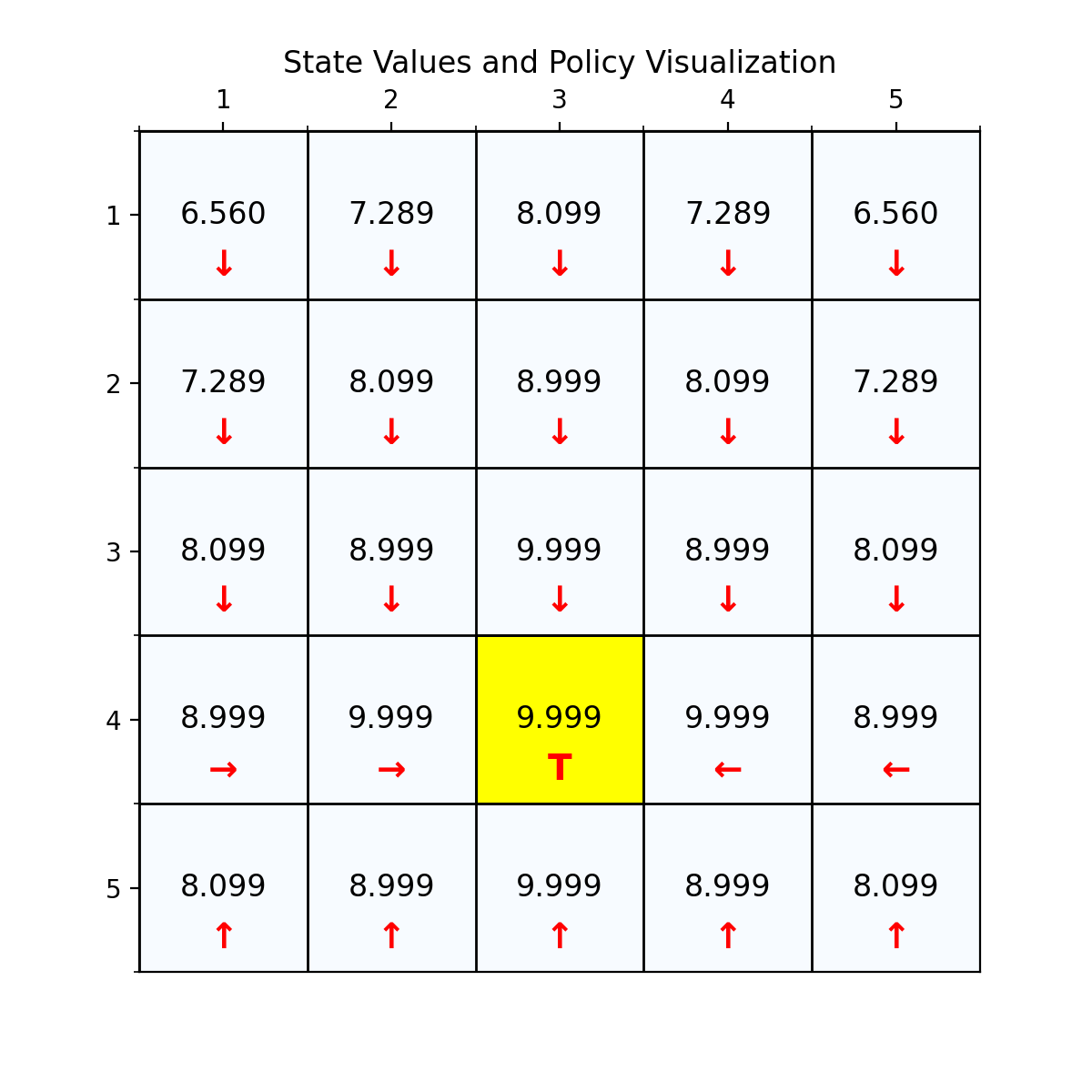
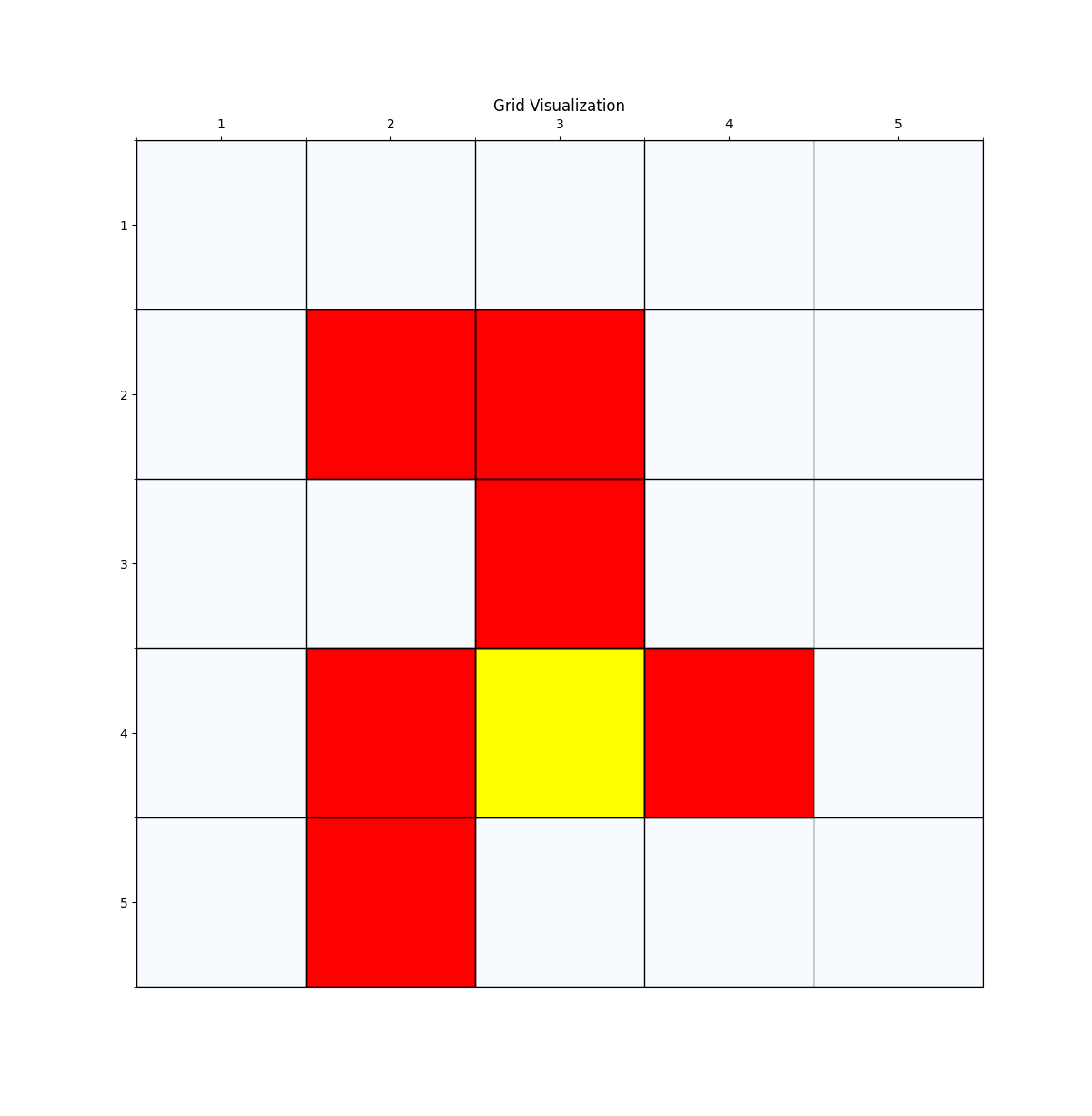
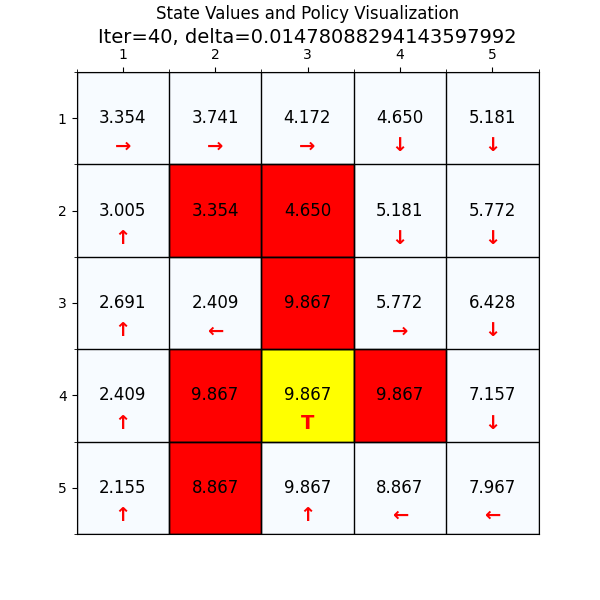
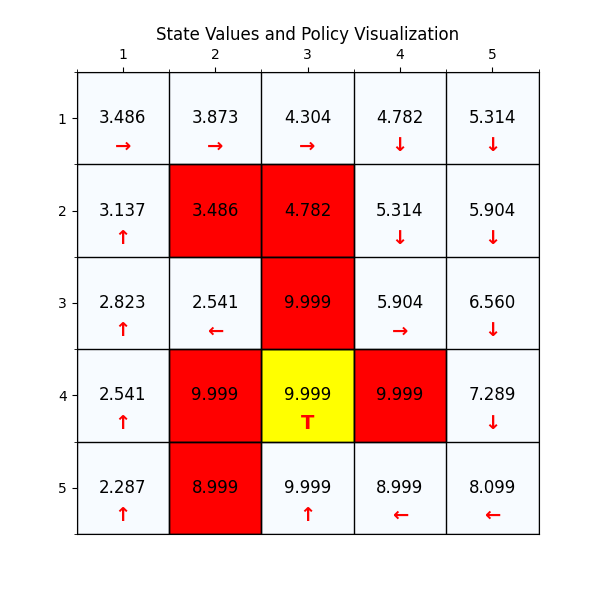
四、复杂的网格世界例子
下面我们换一个复杂的网格世界,看下value 迭代算法怎么找到最优路径。
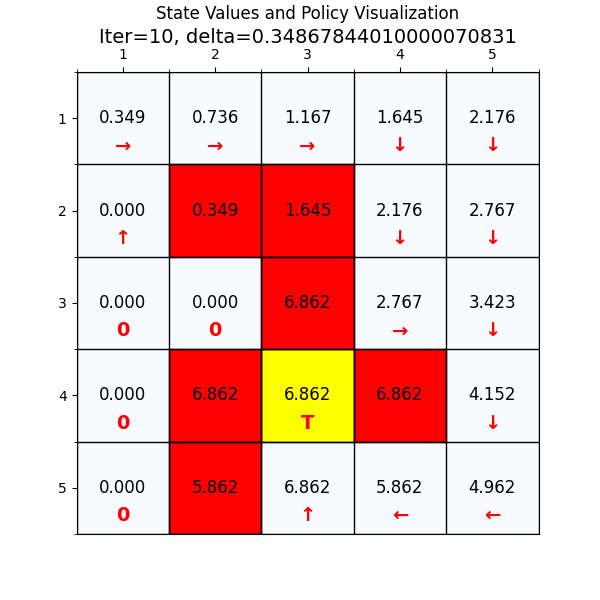
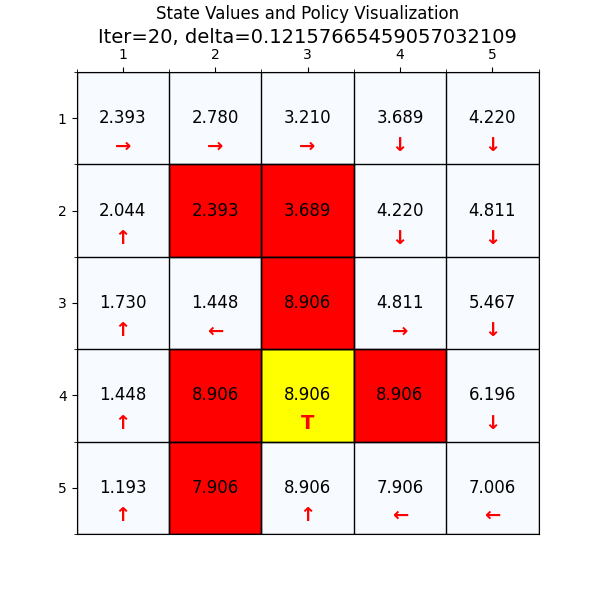
如图4所示,这个就是我们网格世界的升级版GridV3,这个和上个网格的区别是,增加了禁止区域(红色网格,agent进入之后会获得的奖励分数是负的),
增加了边界检测(agent试图突破边界时,获得的奖励也是负的)。
五、思考与总结
通过这两个例子和上节的算法讲解,我们可以完全理解算法的python实现了。
- 最重要的是通过value 迭代算法理解强化学习中的利用Bootstrap思想来优化策略,完全不需要外界的标注数据。
(这个思考点留给刚从深度学习转过来的同学,可以参考这篇文章 为什么强化学习不需要标注样本?) - 另外就是熟悉强化学习中交替进行value update和policy update的套路,后面学习的算法形式上都是如此,
具体改变在于使用什么模型和方法进行update,但是形式并没有发生变化。
好了,下一篇是关于policy 迭代算法和实现!



